核技巧
支持向量机按照分类的数据进行分类:
- 线性支持向量机
- 非线性支持向量机
在支持向量机中,支持向量的作用是减少了计算量。核技巧的作用是使得支持向量机在数据线性不可分的情况下也可以应用,将支持向量机推广到了非线性。
支持向量机的本质是求得一个平面$\omega x + b = 0$,并用这个平面将数据尽量的分类开来。支持向量机结果只能给出分类结果,并不能像神经网络一样,给出分类概率。
未应用支持向量机针对的是线性可分数据集合,如果数据是线性不可分的数据,则支持向量机无能为力。不过我们可以人为的经过一些变换将线性不可分的数据集和变为线性可分。例如我们可以将以圆为分界线的数据集合点,园内为$+1$,圆外为$-1$. 针对这种情况,没有用到核技巧的支持向量机无法正确分类。如果将横纵坐标各自平方,数据在此个高维空间就是线性可分的,再利用支持向量机可以进行分类。
针对上面情况,可以总结为将原始空间的数据点的属性(上面是原始数据是二维的,二个属性),经过一些变化变为另外一个空间上(这个空间可以是同维度的,例如上面只是自己和自己平方以下,结果仍然是二维的,也可以是高维度的,并且一般情况下都是高维度的,甚至是无穷维度的,例如高斯核函数对应的希尔伯特空间),这个空间叫做希尔伯特空间。再在希尔伯特空间上应用支持向量机算法,去分类数据。
核技巧的想法是:省去由原始空间变化到希尔伯特空间的步骤。而是直接得到在希尔伯特空间进行内积的结果。
核技巧的想法的可行的原因是,在未使用核技巧的支持向量机的优化函数的一项是由原始空间的向量内机组成的,所以延伸到非线性可分的数据集和中,也可以由希尔伯特空间的向量內积组成。
例子:

其中$x,z$都是原始空间的点,上面的例子(多项式函数的一种)中,只是原始空间中的点自己的属性相互进行加减乘除变换到希尔伯特空间。点$x$的属性$(x_1,x_2)$ 相互的运算得到了希尔伯特空间的点,可以是三维也可以是四维的。
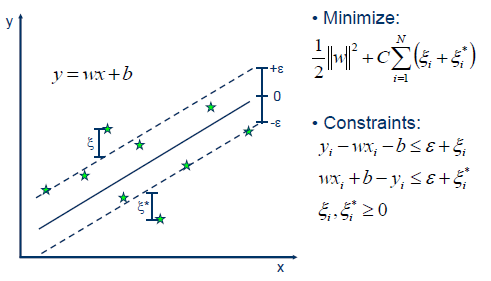
此外,svm 还是可以进行回归预测的,叫做 SVR ,此时的数据已经和之前的用于分类的数据有很大不同,此时的$y_i$ 已经是实数,而并不是原来的离散值,例如$-1,+1$之类的。支持向量的概念任然存在,但是此时考虑到了支持向量以外的点的回归误差。